MEGHÍVÓ

      Szeretettel meghívjuk Szénási Eszter, Török Roland és Tauber Boglárka

                  előadására az Optimalizálási Szeminárium keretében

                         2019. június 20, csütörtök 14:15 - 15:45

                           Helyszín: BME H. épület 406 terem

A szemináriumon Szénási Eszter és Török Roland MSc-s hallgatók, és Tauber Boglárka BSc-s hallgató tartanak előadást a diplomamunkájukról.

Szénási Eszter:

Új keresési irányra épülő belsőpontos algoritmus lineáris optimalizálásra

Absztrakt:

Az előadás keretein belül egy új keresési irányra alapozott teljes Newton-lépéses belsőpontos algoritmust mutatok be lineáris optimalizálási feladatok megoldására. Az eljárás során algebrailag ekvivalens átalakítások segítségével a centrális utat megadó egyenletrendszert változtatjuk meg. Az alábbi függvényt alkalmazzuk a centralitási egyeneletre:

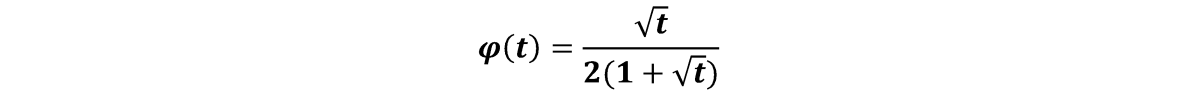
Ezt a függvényt Kheirfam és Haghighi alkalmazta elsőként, lineáris komplementaritási feladatokra. Ez az első lineáris optimalizálásra vonazkotó belsőpontos algoritmus, amely ezzel a speciális keresési iránnyal dolgozik. Newton-módszert használunk az előzőleg kapott rendszerre az új keresési irányok meghatározásának érdekében. Ezt követően a bevezetett algoritmus által meghatározott maximális iteráció számra vonazkotó felső korlátot számítjuk ki. Megmutatjuk, hogy az algoritmus polinomiális komplexitású. Az eredmények numerikus tesztekkel is alátámasztásra kerülnek, konkrét példákon, alkalmazásokon.

Tauber Boglárka:

Humán erőforrás ütemezési feladat megoldása személyes preferenciákkal

Absztrakt:

Az előadásomban egy optimalizálási modellt építek fel, mely egy munkaerő-hozzárendelési feladatot ír le, pontosabban diákmunkák beosztását határozza meg. Ennek nehézsége, hogy nem előre meghatározott műszakokba soroljuk a hallgatókat, hanem ők megadják, hogy egy adott hét napjain mikor érnek rá dolgozni. A beosztást pedig ennek megfelelően kapják, azaz a leadott ráérésükön kívül nem dolgozhatnak.

A probléma egy vegyes egészértékű lineáris programozási feladatként fogalmazható meg, melynek bemenete többek között, hogy a diákok mikor szeretnének dolgozni, valamint, hogy a hallgatókat alkalmazó cég hány munkaóra teljesítését várja el összesen a diákoktól. A nyilvánvaló feltételeken kívül számos olyan feltevés található a modellben, mely kényelmi szempontokat is figyelembe vesz mind a munkavállalók, mind a munkaadók részéről. A modellt az Xpress Solver segítségével implementáltam. A modellt először a munkaadótól kapott, kis méretű adatokon futtattam, ezeken legfeljebb pár perc volt a futásidő. Ezek után egy Pythonban megírt program segítségével generáltam nagy méretű, valósághű adatokat, melyek kielégítették a ráérésekre vonatkozó feltételeket, és ezen paraméterek által meghatározott feladatokat oldottam meg. A modell alkalmasnak bizonyult a valós méretű problémák gyors megoldására, valamint a feltételek ki-, és hozzávehetőségével lehetővé teszi a feltevések priorizálását, így akár hasonló diákmunkák esetén használható is megengedett beosztások készítésére.

Török Roland:

Lineáris komplementaritási problémák numerikus megoldásai

Absztrakt:

A diplomamunka lényege az elégséges LCP-k megoldására szolgáló algoritmusok bemutatása és közülük egyik leprogramozása. Az elméletben működő algoritmusok viszont a numerikus számítások során fellépő hibák miatt nem működnek megfelelően a gyakorlatban, így a megvalósításhoz az adódó problémák kezelése is hozzátartozott. Az LCP-t megoldó algoritmus, azért fontos, hiszen a legtöbb gyakorlati probléma ilyen feladatként írható fel. Gyakorlatban a mechanikában és a közgazdaságban több helyen is előfordulnak LCP-k. Több különböző algoritmus létezik ilyen problémák megoldására, mely módszereket 3 osztályba soroljuk. A pivot, a belső pontos és a konstruktív módszerek ezek. Implementálásra a belső pontos algoritmusok közül a primál-duál Newton módszer került. Természetesen ezen algoritmus végességének bizonyítása és lépésszámának egy felső korlátja is be lett mutatva a dolgozatban. Ezután pedig az implementálás során fellépő numerikus problémákról és azok javításáról való értekezés került előtérbe. Végezetül pedig a tesztelés eredményei kerültek bemutatásra.

A program az ALGLIB könyvtár használatával készült, mely LU-felbontást numerikusan nagyon jól tud kezelni. Az általam implementált program a legtöbb 10x10-es problémát nagyon gyorsan és viszonylag jól megoldotta 1 kivétellel a tesztesetekből. 20x20-as problémák közül már történtek a numerikus számítások miatt 1-2 esetben anomáliák, de itt is gyorsan és viszonylag pontosan meg tudta oldani a problémát. 50x50-es esetben hasonlóan a 10x10-es példákhoz szinte az összeset meg tudta oldani a program, azonban ennél nagyobb feladatoknál már problémákba ütközött, ezért ezek már nem kerültek bele a diplomamunkába. Összehasonlításként az Xpress programcsomag beépített NLP megoldóját is teszteltem, mely azonban az összes esetet megoldotta és az 50x50-es esetben jelentősen gyorsabban is.