MEGHÍVÓ
Szeretettel meghívjuk Bozóki Sándor előadására
az Optimalizálási Szeminárium keretében
2019. március 14-én csütörtökön, 14:15-15:45 óráig
Helyszín: BME H épület H. 406-os terem
Előadó:
Bozóki Sándor MTA SZTAKI Mérnöki és Üzleti Intelligencia Kutatólaboratórium, Operációkutatás és Döntési Rendszerek Kutatócsoport; Budapesti Corvinus Egyetem, Operációkutatás és Aktuáriustudományok Tanszék
Nemlineáris egyenletrendszerek megoldása közelítő polinomok segítségével
Absztrakt: Számos matematikai, optimalizálási, mérnöki és gazdasági probléma egy nemlineáris egyenletrendszer megoldását igényli, ahol megoldás alatt az összes (valós) gyök megtalálását értjük. A feladat nehéz, még abban a speciális esetben is, ha minden egyenlet egy többváltozós polinom. Egy egyenletrendszert négyzetesnek nevezünk, ha a változók és az egyenletek száma megegyezik.
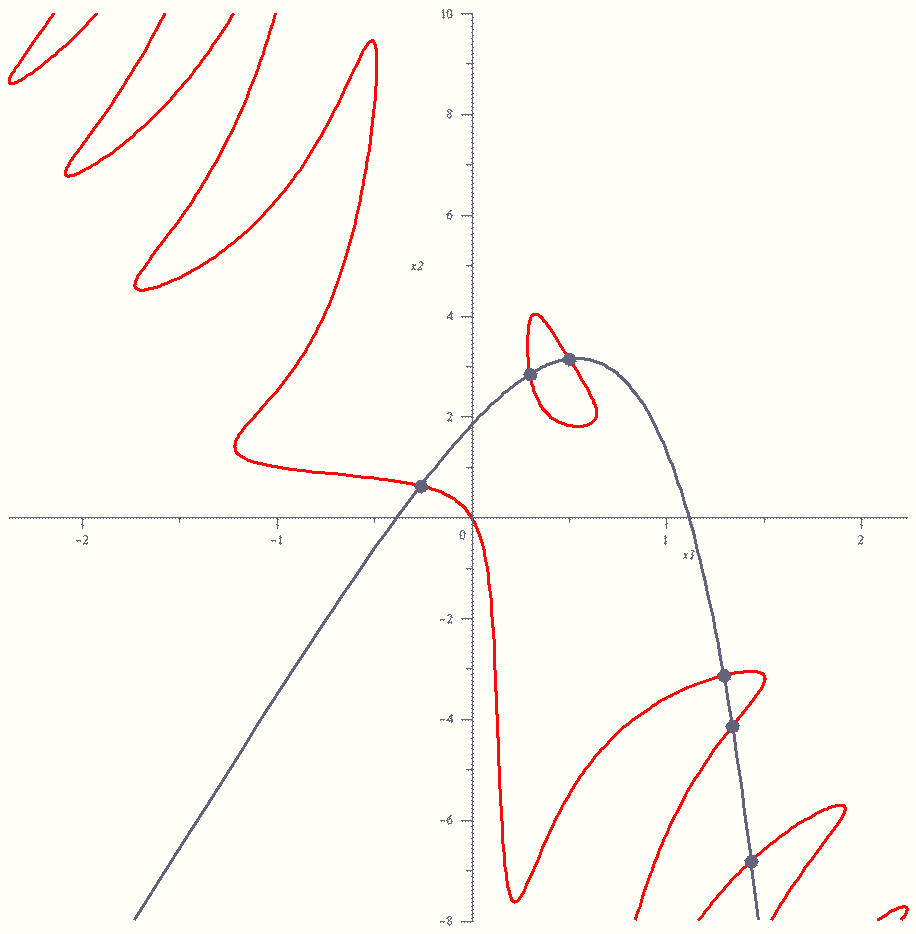
Az előadásban egy módszert javasolok olyan négyzetes nemlineáris egyenletrendszerek megoldására, amelyekben a nempolinomiális egyenletekben szereplő transzcendens függvények jól közelíthetők a Taylor-soraikkal vagy más approximációs polinomokkal. Tapasztalataim szerint ekkor a közelítő többváltozós polinomrendszer homotópiás módszerrel számolt megoldásai alkalmas indulópontokként szolgálnak az eredeti egyenletrendszer Newton-iterációval történő megoldásához. Az eljárást példákkal illusztrálom.